在人工智能與機(jī)器學(xué)習(xí)領(lǐng)域，線性回歸是最基礎(chǔ)、最核心的算法之一，它不僅是理解更復(fù)雜模型的基石，也是許多實(shí)際應(yīng)用的起點(diǎn)。本文旨在系統(tǒng)梳理線性回歸，特別是多元線性回歸的基本概念、最優(yōu)解求解方法，并結(jié)合有監(jiān)督機(jī)器學(xué)習(xí)的工作流程，通過Jupyter Notebook的實(shí)踐視角，為人工智能基礎(chǔ)軟件開發(fā)提供清晰的指引。

一、基本概念：什么是有監(jiān)督機(jī)器學(xué)習(xí)與線性回歸

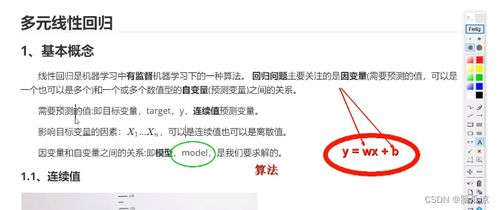
有監(jiān)督機(jī)器學(xué)習(xí)是指模型從已標(biāo)注的訓(xùn)練數(shù)據(jù)（即包含輸入特征和對(duì)應(yīng)輸出標(biāo)簽的數(shù)據(jù)集）中學(xué)習(xí)規(guī)律，并用于對(duì)新數(shù)據(jù)進(jìn)行預(yù)測(cè)。線性回歸正是一種典型的有監(jiān)督學(xué)習(xí)算法。其核心思想是：假設(shè)目標(biāo)變量（因變量）與一個(gè)或多個(gè)特征變量（自變量）之間存在線性關(guān)系，并試圖找到一個(gè)線性方程來最佳地?cái)M合已知數(shù)據(jù)點(diǎn)。

簡(jiǎn)單線性回歸：涉及一個(gè)自變量（特征）和一個(gè)因變量（目標(biāo)），形式為 \( y = w1 x + b \)，其中 \( w1 \) 是權(quán)重（斜率），\( b \) 是偏置（截距）。

多元線性回歸：這是本文的重點(diǎn)。當(dāng)結(jié)果受到多個(gè)因素影響時(shí)，我們使用多元線性回歸，其方程擴(kuò)展為：

\[ y = w1 x1 + w2 x2 + ... + wn xn + b \]

其中，\( y \) 是預(yù)測(cè)值，\( x1, x2, ..., xn \) 是n個(gè)特征，\( w1, w2, ..., wn \) 是對(duì)應(yīng)的權(quán)重（模型參數(shù)），\( b \) 是全局偏置。模型的目標(biāo)是學(xué)習(xí)到一組最佳的 \( w \) 和 \( b \)。

二、核心目標(biāo)：尋找最優(yōu)解

“最優(yōu)解”指的是能夠使模型的預(yù)測(cè)值與真實(shí)值之間誤差最小的那組參數(shù)。在線性回歸中，我們通常使用最小二乘法作為衡量誤差的標(biāo)準(zhǔn)，即最小化所有數(shù)據(jù)點(diǎn)上預(yù)測(cè)值與真實(shí)值之差的平方和，這個(gè)和被稱為損失函數(shù)（或成本函數(shù)）。對(duì)于多元線性回歸，損失函數(shù) \( J \) 表示為：

\[ J(w, b) = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2 \]

其中，\( m \) 是樣本數(shù)量，\( \hat{y}^{(i)} \) 是第 \( i \) 個(gè)樣本的預(yù)測(cè)值，\( y^{(i)} \) 是其真實(shí)值。

求解這個(gè)最優(yōu)解主要有兩種方法：

1. 解析解（正規(guī)方程）：通過數(shù)學(xué)公式直接計(jì)算參數(shù)。對(duì)于多元線性回歸，公式為 \( \theta = (X^T X)^{-1} X^T y \)，其中 \( \theta \) 是包含所有權(quán)重和偏置的參數(shù)向量。這種方法在特征數(shù)量不多時(shí)計(jì)算高效，但特征維度很高或矩陣不可逆時(shí)可能不適用。
2. 數(shù)值優(yōu)化解（梯度下降）：這是一種迭代方法。通過計(jì)算損失函數(shù)關(guān)于每個(gè)參數(shù)的梯度（導(dǎo)數(shù)），然后沿梯度反方向（即下降最快的方向）更新參數(shù)，逐步逼近最小值點(diǎn)。這是機(jī)器學(xué)習(xí)中最常用、最核心的優(yōu)化算法，能夠處理大規(guī)模數(shù)據(jù)集和復(fù)雜模型。

三、實(shí)踐工具：Jupyter Notebook在人工智能基礎(chǔ)軟件開發(fā)中的角色

Jupyter Notebook是一個(gè)開源的Web應(yīng)用程序，允許我們創(chuàng)建和共享包含實(shí)時(shí)代碼、可視化、方程和敘述性文本的文檔。它在人工智能基礎(chǔ)學(xué)習(xí)和軟件開發(fā)中不可或缺：

• 交互式探索：可以逐行或分塊運(yùn)行代碼（如Python），立即看到結(jié)果，非常適合數(shù)據(jù)加載、預(yù)處理、模型訓(xùn)練和可視化的每一步探索。
• 可視化呈現(xiàn)：可以直接內(nèi)嵌繪制損失函數(shù)下降曲線、數(shù)據(jù)分布散點(diǎn)圖、回歸擬合線等，直觀理解模型行為和性能。
• 文檔與報(bào)告：將代碼、運(yùn)行結(jié)果、數(shù)學(xué)公式（使用LaTeX）和文字說明結(jié)合在一個(gè)筆記本中，形成結(jié)構(gòu)清晰的工作筆記或項(xiàng)目報(bào)告，便于知識(shí)沉淀和團(tuán)隊(duì)協(xié)作。
• 原型快速開發(fā)：在構(gòu)建正式軟件或系統(tǒng)前，可在Notebook中快速驗(yàn)證想法、測(cè)試算法和調(diào)整參數(shù)。

四、工作筆記與開發(fā)流程示例

在“人工智能工作筆記0040”中，一個(gè)典型的多元線性回歸項(xiàng)目可能包含以下步驟：

1. 環(huán)境設(shè)置與數(shù)據(jù)導(dǎo)入：在Jupyter Notebook中導(dǎo)入必要的庫(kù)（如NumPy, Pandas, Matplotlib, Scikit-learn）。
2. 數(shù)據(jù)理解與預(yù)處理：加載數(shù)據(jù)集，使用Pandas進(jìn)行探索性分析；處理缺失值；對(duì)分類特征進(jìn)行編碼（如獨(dú)熱編碼）；必要時(shí)進(jìn)行特征縮放（如標(biāo)準(zhǔn)化），以加速梯度下降收斂。
3. 模型構(gòu)建與訓(xùn)練：

• 從零實(shí)現(xiàn)：使用NumPy定義模型函數(shù)、損失函數(shù)和梯度下降算法，手動(dòng)訓(xùn)練模型，深入理解原理。

• 使用框架：調(diào)用Scikit-learn的LinearRegression或SGDRegressor，快速構(gòu)建和訓(xùn)練模型。

1. 評(píng)估與優(yōu)化：在測(cè)試集上評(píng)估模型性能，使用指標(biāo)如均方誤差（MSE）、決定系數(shù)（R2）。分析結(jié)果，可能需要返回進(jìn)行特征工程或調(diào)整正則化（如引入嶺回歸或Lasso以防止過擬合）。
2. 結(jié)果可視化與解釋：繪制特征與預(yù)測(cè)值的關(guān)系圖；對(duì)于高維模型，可繪制學(xué)習(xí)曲線或關(guān)鍵特征的權(quán)重條形圖，以解釋模型。
3. 與筆記：記錄本次實(shí)驗(yàn)的關(guān)鍵發(fā)現(xiàn)、遇到的問題及解決方案、參數(shù)設(shè)置和最終模型性能。這為后續(xù)的模型迭代或更復(fù)雜的項(xiàng)目（如邏輯回歸、神經(jīng)網(wǎng)絡(luò)）奠定了基礎(chǔ)。

結(jié)論

線性回歸，尤其是多元線性回歸，為我們提供了一把打開有監(jiān)督機(jī)器學(xué)習(xí)大門的鑰匙。理解其基本概念、掌握求解最優(yōu)解的數(shù)學(xué)原理和優(yōu)化方法，是構(gòu)建更復(fù)雜AI模型的基石。而Jupyter Notebook作為強(qiáng)大的交互式工具，極大地促進(jìn)了從理論到實(shí)踐的轉(zhuǎn)化，使得學(xué)習(xí)、實(shí)驗(yàn)和軟件開發(fā)過程更加高效和直觀。在人工智能基礎(chǔ)軟件開發(fā)的旅程中，扎實(shí)掌握這些基礎(chǔ)組件，并養(yǎng)成撰寫清晰工作筆記的習(xí)慣，將為后續(xù)的深入探索奠定堅(jiān)實(shí)的基礎(chǔ)。